Chaos Game
Barnsley fern
-

-
clc; clear; close all %% Parameters maxIter = 1e6; % Max number of dice rolls gifFilename = 'matlab_chaos_game_gif_fern.gif'; %% Initialization xx = zeros(1, maxIter); yy = zeros(1, maxIter); x_0 = [0; 0]; %% Generating points frameIter = 1; % Start with the first frame for i = 1:maxIter % Randomly choose a transformation randx = randi([1 100]); if randx == 1 x_0 = [0 0; 0 0.16] * x_0; elseif randx <= 86 x_0 = [0.85 0.04; -0.04 0.85] * x_0 + [0; 1.60]; elseif randx <= 93 x_0 = [0.20 -0.26; 0.23 0.22] * x_0 + [0; 1.60]; else x_0 = [-0.15 0.28; 0.26 0.24] * x_0 + [0; 0.44]; end % Store the generated point xx(1, i) = x_0(1); yy(1, i) = x_0(2); % Save frames for powers of 2 if i == frameIter || i == maxIter % Plot the points figure(1); clf; set(gcf, 'Position', [100, 100, 800, 800], 'Color', 'none'); % Make figure background transparent ax = axes('Position', [0 0 1 1], 'Visible', 'off'); % Remove axes hold on; sz = 1; c = linspace(1, 100, i); scatter(xx(1:i), yy(1:i), sz, c, 'filled'); % Add title text(0, 10.5, ['Chaos Game - Iteration ' num2str(i)], ... 'HorizontalAlignment', 'center', 'FontSize', 14, 'Color', 'k'); axis equal; axis([-3 3 0 10]); % Adjust the axis limits for better visualization drawnow; % Capture frame and write to GIF frame = getframe(gcf); img = frame2im(frame); [imind, cm] = rgb2ind(img, 256); if i == 1 imwrite(imind, cm, gifFilename, 'gif', 'Loopcount', inf, 'DelayTime', 0.3); else imwrite(imind, cm, gifFilename, 'gif', 'WriteMode', 'append', 'DelayTime', 0.3); end % Update to the next power of 4 frameIter = frameIter * 4; end end disp(['GIF saved as ', gifFilename]);
Regular Polygons
-

-
%% Purpose: General case of Chaos Game for N vertex Regular Poly clc; clear; close all; %% Input n = 6; % number of vertices r = 1; % scaling of unit circle c = [0, 0]; % center of circle divisionFactor = [2.5 2.5]; % Case [d d]: x_new = (x_old + vertex)/d % Case [a b]: d = a + (b - a)*rand(1) % x_new = (x_old + vertex)/d % NOTE: for d<2 system explodes diceRepeatCheck = [1 1]; % min max of number of consecutive repeated dice rolls numofDiceRolles = 1000000; % number of points generated plotBoarderToggle = false; gifFilename = 'matlab_chaos_game_reg_poly.gif'; %% Make Regular Poly vertexCoord = RegularPolyGenerator(n, r, c); %% Start the Game % Grid xx = zeros(1, numofDiceRolles); yy = zeros(1, numofDiceRolles); % Initial Point x_0 = [0, 0]; %% Start Rolling frameIter = 1; % Start with the first frame (power of 2) for i = 1:numofDiceRolles % Roll the N-sided dice dice_number = randi([1 n]); closest_vertex = vertexCoord(dice_number, :); % Calculate division factor minF = divisionFactor(1); maxF = divisionFactor(2); d = minF + (maxF - minF) * rand(1); % Compute new point x_0 = (x_0 + closest_vertex) / d; xx(1, i) = x_0(1); yy(1, i) = x_0(2); % Save frames for GIF at powers of 2 if i == frameIter || i == numofDiceRolles % Plot the points figure(1); clf; set(gcf, 'Position', [100, 100, 800, 800], 'Color', 'k'); % Black background hold on; % Plot the polygon in yellow if plotBoarderToggle plotBoarder(vertexCoord, n, 'y'); end % Plot points in cyan scatter(xx(1:i), yy(1:i), 1, 'c', 'filled'); axis equal; set(gca, 'Color', 'k', 'XColor', 'none', 'YColor', 'none'); % Black axes background drawnow; % Capture frame and write to GIF frame = getframe(gcf); img = frame2im(frame); [imind, cm] = rgb2ind(img, 256); if i == 1 imwrite(imind, cm, gifFilename, 'gif', 'Loopcount', inf, 'DelayTime', 0.3); else imwrite(imind, cm, gifFilename, 'gif', 'WriteMode', 'append', 'DelayTime', 0.3); end % Update to the next power of 2 frameIter = frameIter * 2; end end disp(['GIF saved as ', gifFilename]); %% Functions function plotBoarder(vertexCoord, n, color) hold on; for i = 1:n-1 line(vertexCoord(i:i+1, 1), vertexCoord(i:i+1, 2), 'color', color, 'LineWidth', 1.5); end line([vertexCoord(1, 1), vertexCoord(n, 1)], ... [vertexCoord(1, 2), vertexCoord(n, 2)], 'color', color, 'LineWidth', 1.5); end function vertexCoord = RegularPolyGenerator(n, r, c) alpha = 0; cNodeAngle = 2 * pi / n; vertexCoord = zeros(n, 2); for i = 1:n vertexCoord(i, :) = r * [sin(alpha), cos(alpha)] + c; alpha = alpha + cNodeAngle; end end
Sierpinski Triangle
-
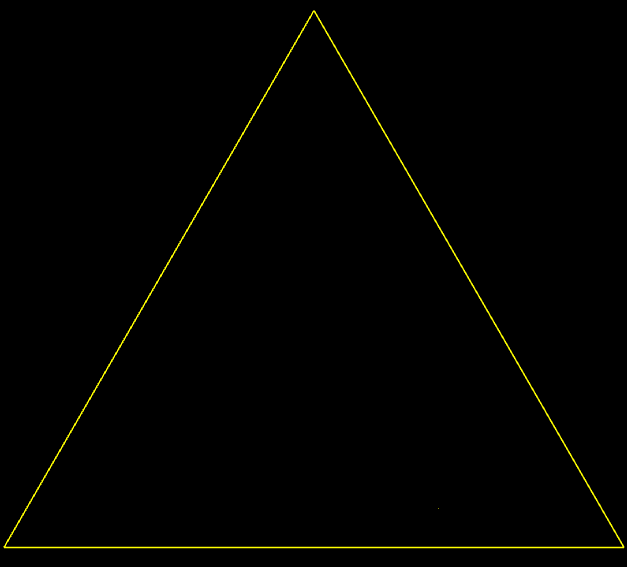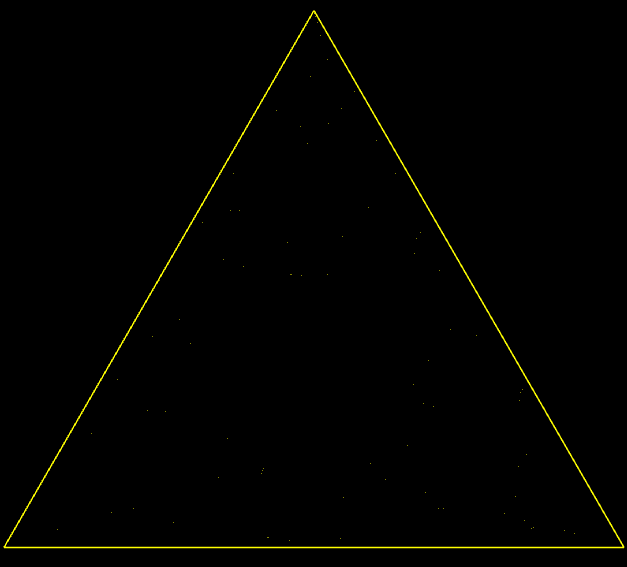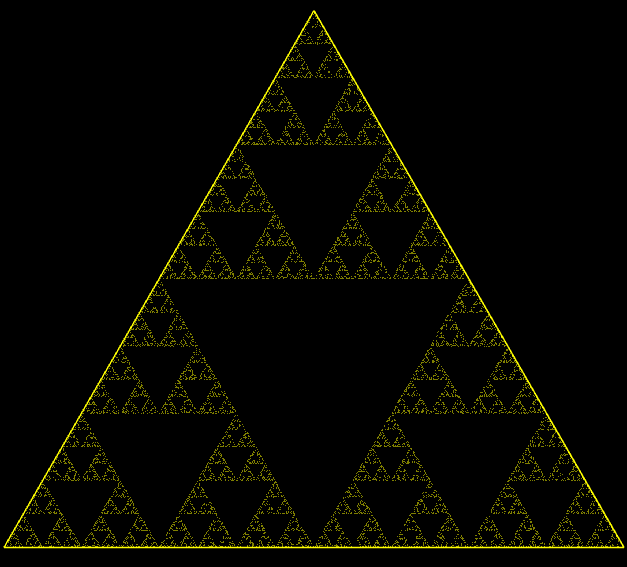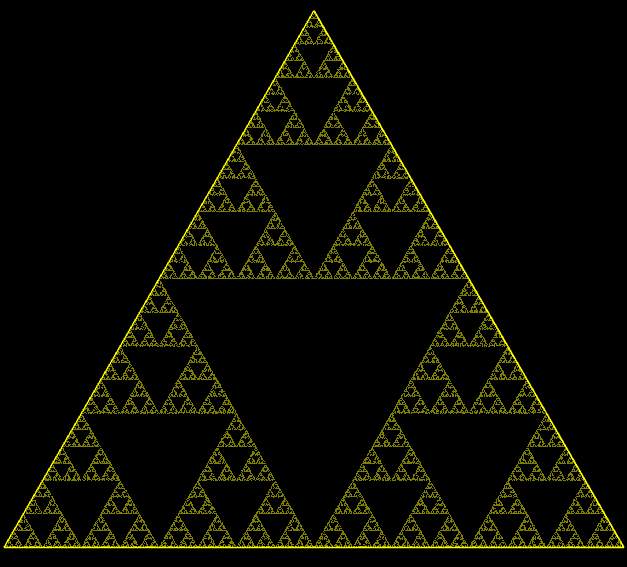
-
clc; clear; close all %% Parameters maxIter = 1e6; % Max number of dice rolls gifFilename = 'matlab_chaos_game_eq_triangle.gif'; %% Triangle Vertices v1.x = 0; v1.y = 0; v2.x = 1; v2.y = 0; v3.x = 1/2; v3.y = sqrt(3)/2; %% Pick Random Initial Point Inside the Triangle r1 = rand(); r2 = rand(); if r1 + r2 > 1 r1 = 1 - r1; r2 = 1 - r2; end % Compute the random point as a linear combination of the vertices x0 = (1 - r1 - r2) * [v1.x, v1.y] + ... r1 * [v2.x, v2.y] + ... r2 * [v3.x, v3.y]; %% Grid for storing points xx = zeros(1, maxIter); yy = zeros(1, maxIter); %% Generating points closest_v = [0, 0]; frameIter = 1; for i = 1:maxIter % Randomly select a vertex based on dice roll dice_number = randi([1, 6]); switch dice_number case {1, 2} closest_v = v1; case {3, 4} closest_v = v2; case {5, 6} closest_v = v3; end % Compute the midpoint x0 = (x0 + [closest_v.x, closest_v.y]) ./ 2; xx(1, i) = x0(1); yy(1, i) = x0(2); % Save frames for powers of 2 if i == frameIter || i == maxIter figure(1); clf; set(gcf, 'Position', [100, 100, 800, 800], 'Color', 'k'); % Black background hold on; % Plot the triangle in yellow line([v1.x, v2.x], [v1.y, v2.y], 'color', 'y', 'LineWidth', 1.5); line([v1.x, v3.x], [v1.y, v3.y], 'color', 'y', 'LineWidth', 1.5); line([v2.x, v3.x], [v2.y, v3.y], 'color', 'y', 'LineWidth', 1.5); % Plot points in yellow scatter(xx(1:i), yy(1:i), 1, 'y', 'filled'); axis equal; set(gca, 'Color', 'k', 'XColor', 'none', 'YColor', 'none'); % Black axes background drawnow; % Capture frame and write to GIF frame = getframe(gcf); img = frame2im(frame); [imind, cm] = rgb2ind(img, 256); if i == 1 imwrite(imind, cm, gifFilename, 'gif', 'Loopcount', inf, 'DelayTime', 0.3); else imwrite(imind, cm, gifFilename, 'gif', 'WriteMode', 'append', 'DelayTime', 0.3); end % Update to the next power of 3 frameIter = frameIter * 3; end end disp(['GIF saved as ', gifFilename]);