Publications

Preprint

2026

1. CDC

   

   A Passivity-Based Analysis of First-Order Momentum-Based Methods

   Sepehr Moalemi, and James R. Forbes

   To Appear in the IEEE Conference on Decision and Control (CDC)

   Abstract PDF BibTeX

   This paper presents a discrete-time passivity-based analysis of first-order momentum-based methods for a class of functions whose gradient has lower and upper sector bounds of \(0\) and \(L\), respectively. Through a loop transformation, it is shown that momentum-based methods can be represented as a passive controller in negative feedback with an output strictly passive (OSP) system. The weak passivity theorem is then used to derive explicit hyperparameter conditions under which the shifted gradient asymptotically vanishes. Under an additional assumption that requires the existence of a unique stationary point and excludes arbitrarily small gradients far from that point, convergence of the iterates to the global minimizer is established.

   @inproceedings{moalemi_forbes_momentum_passive_cdc,
     author = {Moalemi, Sepehr and Forbes, James R.},
     title = {A Passivity-Based Analysis of First-Order Momentum-Based Methods},
     booktitle = {To Appear in the IEEE Conference on Decision and Control (CDC)},
     year = {2026},
     eprint = {2608.05492},
     archiveprefix = {arXiv},
     primaryclass = {eess.SY},
     url = {https://arxiv.org/abs/2608.05492},
   }

2. CDC

   

   Performance-Guaranteed Reference Tracking With Power Directionality Constraints: Application to Controlled Stochastic Watersheds

   Jonathan Shell, Sepehr Moalemi, Branko Kerkez, and Jeff Scruggs

   To Appear in the IEEE Conference on Decision and Control (CDC)

   Abstract PDF BibTeX

   Modern stormwater infrastructure faces increased demands that require a corresponding increase in capacity. Traditionally, these demands have been met by constructing new infrastructure assets, which is a costly endeavor. More recently, many system operators have achieved great success in employing feedback control techniques to improve system performance. However, the resulting closed-loop system exhibits power directionality constraints that introduce nonlinear constraints in feedback synthesis. In this work, we develop a stochastic control synthesis procedure with provable performance bounds on mean-square reference tracking for a general class of problems in which power directionality constraints arise. The proposed method is then applied to a flood mitigation example using a numerical model of a real-world smart water system. The key result is an extension of the performance-guaranteed control (PGC) framework, which was originally designed for disturbance rejection, to accommodate reference tracking control objectives.

   @inproceedings{shell_moalemi_kerkez_scruggs_pgc_pdc_cdc,
     author = {Shell, Jonathan and Moalemi, Sepehr and Kerkez, Branko and Scruggs, Jeff},
     title = {Performance-Guaranteed Reference Tracking With Power Directionality Constraints: Application to Controlled Stochastic Watersheds},
     booktitle = {To Appear in the IEEE Conference on Decision and Control (CDC)},
     year = {2026},
     archiveprefix = {arXiv},
     primaryclass = {eess.SY},
     url = {https://arxiv.org/abs/2608.20120},
   }

Published

2025

1. TAC

   

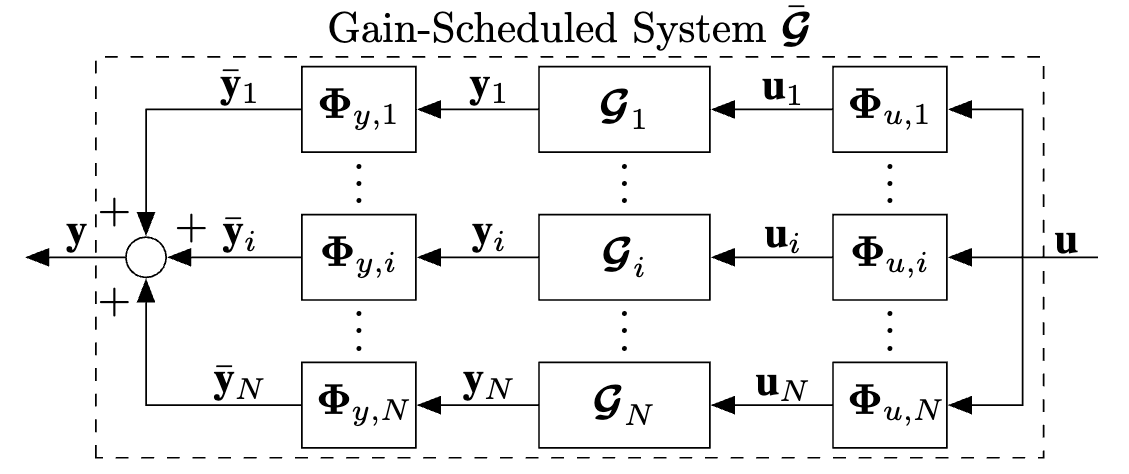   Matrix-Scheduling of QSR-Dissipative Systems

   Sepehr Moalemi, and James R. Forbes

   IEEE Transactions on Automatic Control (TAC)

   Abstract PDF Code BibTeX

   This paper considers gain-scheduling of QSR-dissipative subsystems using scheduling matrices. The corresponding QSR-dissipative properties of the overall matrix-gain-scheduled system, which depends on the QSR properties of the subsystems scheduled, are explicitly derived. The use of scheduling matrices is a generalization of the scalar scheduling signals used in the literature, and allows for greater design freedom when scheduling systems, such as in the case of gain-scheduled control. Furthermore, this work extends the existing gain-scheduling results to a broader class of QSR-dissipative systems. The matrix-scheduling of important special cases, such as passive, input strictly passive, output strictly passive, finite \(\mathcal{L}_2\) gain, very strictly passive, and conic systems are presented. The proposed gain-scheduling architecture is used in the context of controlling a planar three-link robot subject to model uncertainty. A novel control synthesis technique is used to design QSR-dissipative subcontrollers that are gain-scheduled using scheduling matrices. Numerical simulation results highlight the greater design freedom of scheduling matrices, leading to improved performance.

   @article{moalemi_forbes_qsr_gs_tac,
     author = {Moalemi, Sepehr and Forbes, James R.},
     title = {Matrix-Scheduling of QSR-Dissipative Systems},
     journal = {IEEE Transactions on Automatic Control (TAC)},
     year = {2025},
     volume = {70},
     number = {8},
     pages = {5286-5300},
     doi = {10.1109/TAC.2025.3542329},
   }

2. ACC

   

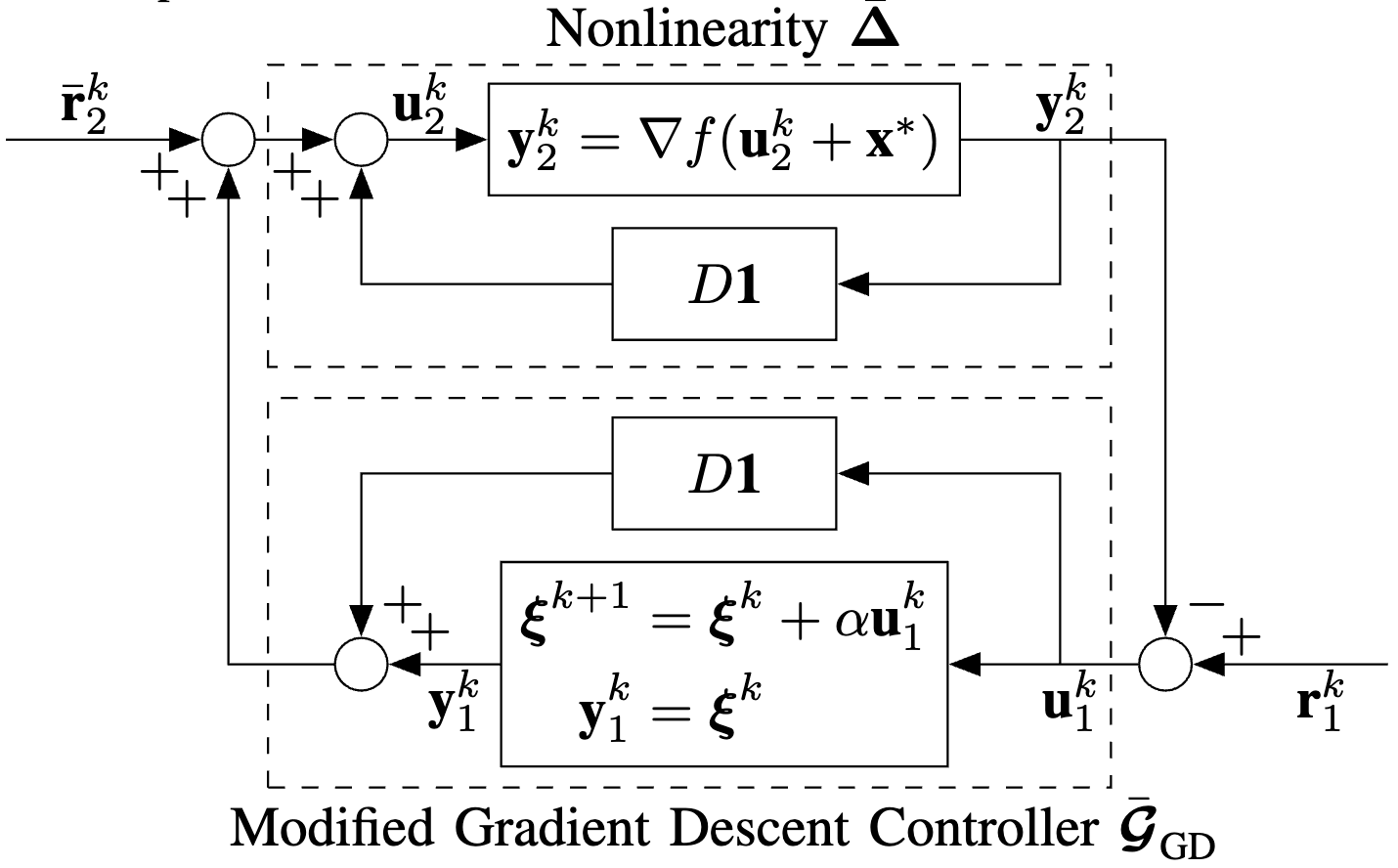   Input-Output Stability of Gradient Descent: A Discrete-Time Passivity-Based Approach

   Sepehr Moalemi, and James R. Forbes

   American Control Conference (ACC)

   Abstract PDF Slides BibTeX

   This paper presents a discrete-time passivity-based analysis of the gradient descent method for a class of functions with sector-bounded gradients. Using a loop transformation, it is shown that the gradient descent method can be interpreted as a passive controller in negative feedback with a very strictly passive system. The passivity theorem is then used to guarantee input-output stability, as well as the global convergence, of the gradient descent method. Furthermore, provided that the lower and upper sector bounds are not equal, the input-output stability of the gradient descent method is guaranteed using the weak passivity theorem for a larger choice of step size. Finally, to demonstrate the utility of this passivity-based analysis, a new variation of the gradient descent method with variable step size is proposed by gain-scheduling the input and output of the gradient.

   @inproceedings{moalemi_forbes_gd_passive_acc,
     author = {Moalemi, Sepehr and Forbes, James R.},
     title = {Input-Output Stability of Gradient Descent: A Discrete-Time Passivity-Based Approach},
     booktitle = {American Control Conference (ACC)},
     year = {2025},
     pages = {924--929},
     doi = {10.23919/ACC63710.2025.11107445},
   }

2024

1. CCTA

   

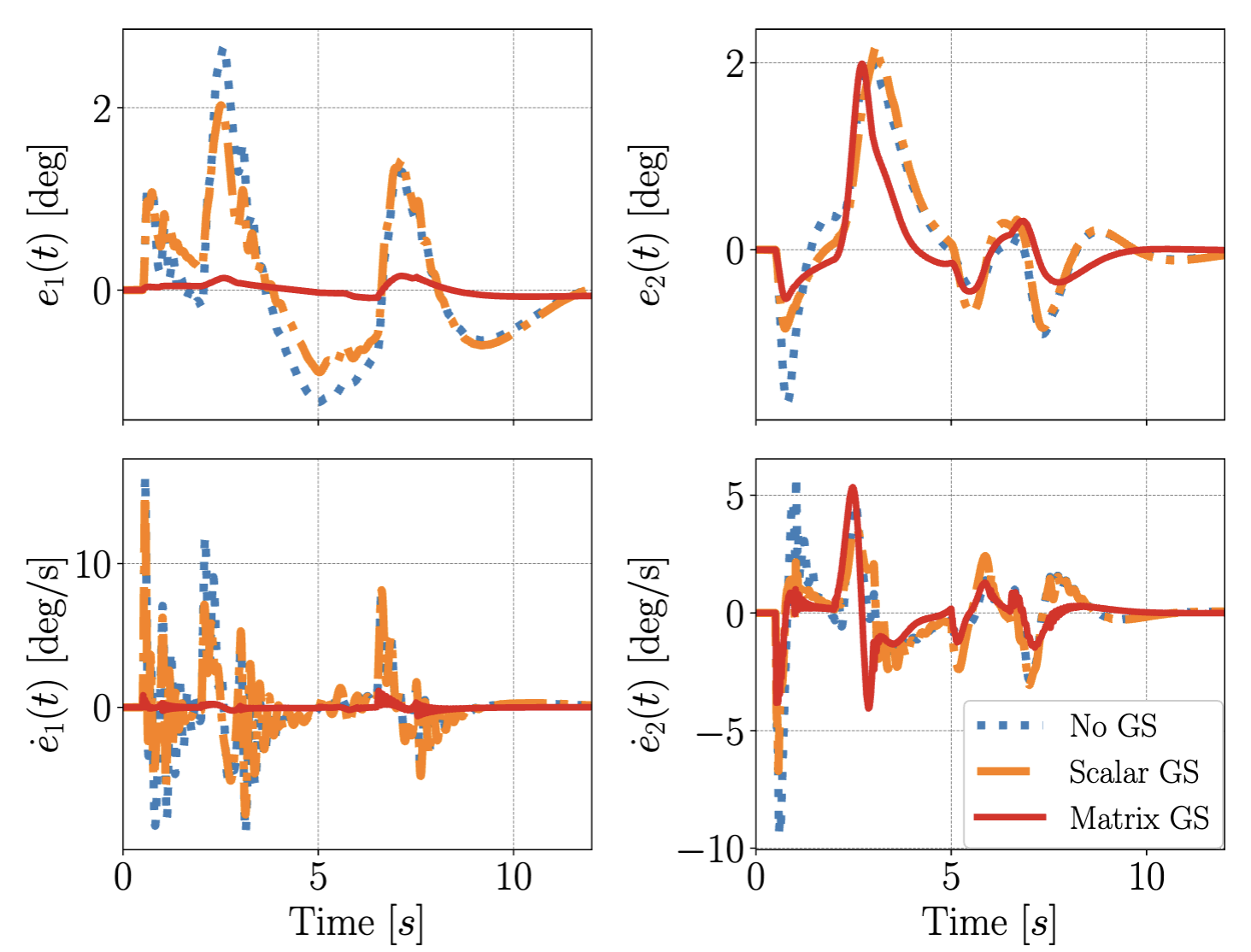   Passivity-Based Gain-Scheduled Control with Scheduling Matrices

   Sepehr Moalemi, and James R. Forbes

   IEEE Conference on Control Technology and Applications (CCTA)

   Abstract PDF Code Slides BibTeX

   This paper considers gain-scheduling of very strictly passive (VSP) subcontrollers using scheduling matrices. The use of scheduling matrices, over scalar scheduling signals, realizes greater design freedom, which in turn can improve closed-loop performance. The form and properties of the scheduling matrices such that the overall gain-scheduled controller is VSP are explicitly discussed. The proposed gain-scheduled VSP controller is used to control a rigid two-link robot subject to model uncertainty where robust input-output stability is assured via the passivity theorem. Numerical simulation results highlight the greater design freedom, resulting in improved performance, when scheduling matrices are used over scalar scheduled signals.

   @inproceedings{moalemi_forbes_vsp_gs_ccta,
     author = {Moalemi, Sepehr and Forbes, James R.},
     title = {Passivity-Based Gain-Scheduled Control with Scheduling Matrices},
     booktitle = {IEEE Conference on Control Technology and Applications (CCTA)},
     pages = {7--13},
     year = {2024},
     doi = {0.1109/CCTA60707.2024.10666540},
   }

Theses

2025

1. Master's Thesis

   

   Input-Output Stability of First-Order Optimization Algorithms: A Passivity-Based Gain-Scheduling Approach

   Sepehr Moalemi

   McGill University

   Abstract PDF Website BibTeX

   This thesis considers the stability of first-order optimization algorithms, such as gradient descent (GD) and its accelerated variants, using control theory. The control interpretation of such algorithms consists of casting them as a Lur'e problem, where the algorithm is represented as the interconnection of a linear controller in negative feedback with the gradient. Consequently, standard input-output theory, in particular, the Passivity Theorem, can be used to analyze the input-output stability of the interconnection. This passivity-based approach is particularly useful, as it is robust to model uncertainties, such as gradient uncertainty that does not violate passivity. Moreover, the stability of optimization algorithms with varying hyperparameters can be analyzed through the lens of passivity-based gain-scheduling techniques. The novel contributions of this thesis come in two parts.First, it is shown that GD, Polyak's heavy ball (HB), Nesterov's accelerated gradient (NAG), and triple momentum (TM) methods can each be represented as a passive controller in negative feedback with the gradient to be minimized. As such, for a class of functions with sector-bounded gradient, the Passivity Theorem can be used to guarantee the input-output stability as well as the global convergence of these algorithms. Furthermore, compared with existing results, this approach provides a tighter upper bound on the largest allowable step size by guaranteeing the input-output stability of the GD controller.Second, this thesis introduces the gain-scheduling of discrete-time quadratic supply rate (QSR)-dissipative subsystems. The scheduling functions considered here take the form of matrices, generalizing the scalar scheduling functions used in the literature. Furthermore, this thesis extends existing gain-scheduling results to include a broader class of QSR-dissipative systems. Notably, given that passivity is a special case of QSR-dissipativity, it is shown that the matrix-scheduling of passive subsystems results in an overall passive system. As such, the proposed gain-scheduling architecture, in tandem with the passive GD, HB, NAG, and TM controllers, can be used to represent varying hyperparameters and propose new variations of these algorithms.

   @mastersthesis{moalemi_first_order_optimization_thesis,
     author = {Moalemi, Sepehr},
     title = {Input-Output Stability of First-Order Optimization Algorithms: A Passivity-Based Gain-Scheduling Approach},
     school = {McGill University},
     year = {2025},
   }